はじめに

カルマンフィルター(1),(2)に続いて本エントリーでは、非線形なモデルに対してカルマンフィルターを用いるための方法についてまとめます。本稿で述べる内容については、線形モデルの場合のカルマンフィルターの理解を前提とします。線形モデルの場合のカルマンフィルターについては、過去にまとめておりますのでこちらも是非ご覧下さい。

biocv.hateblo.jp

具体的には、非線形モデルを線形近似する拡張カルマンフィルター(Extended Kalman FIlter : EKF)およびサンプル点を用いて分布を近似する無香カルマンフィルター(Unscented Kalman Filter：UKF)について紹介します。EKFの解説については、日本語の記事もネット上に豊富なので本記事ではどちらかというとUKFの解説に重きを置きたいと思います。

非線形なモデル

以前のエントリーで紹介したとおり、一般のカルマンフィルターでは予測モデルと更新モデルの両方が状態量と制御入力、観測に対して線形のモデルである事を前提に時刻$t$における平均と分散およびカルマンゲインを求める式を導出することが出来ました。ここでは線形でないモデルを考えて、その場合の平均と分散およびカルマンゲインを求める式を導出します。

非線形モデル：

$$ {\bf y_t}=f({\bf y_{t-1}},{ \bf u}_t)+{\bf G}_t{ \bf w}_t \tag{1} $$

$$ {\bf z}_t=g({ \bf y}_t)+{ \bf v}_t \tag{2} $$

$$ \begin{align} { \bf w}_t & \sim N(0,Q_t) \tag{3} \\\ { \bf v}_t & \sim N(0,R_t) \tag{4} \end{align} $$

ここで、$\bf{u_t}$は制御入力、${ \bf G}_t$はノイズのモデル式で${ \bf w}_t$と${ \bf v}_t$はそれぞれ式(3),(4)の通り分散共分散行列がそれぞれ$Q_t$と$R_t$の多正規分布に従うノイズです。また、$\bf{y_t},\bf{z_t},\bf{u_t}$と${ \bf w}_t$と${ \bf v}_t$および${ \bf w}_t$と${ \bf v}_t$同士はtによらず独立であるとします。

EKF

EKFのアイデアはシンプルで、非線形な(1)と(2)も局所的に見ると線形な関数と近似できるのでその近似式さえ求まれば後は通常のKFと同様に扱えるというものです。数学的にはTaylor展開した上で、2次の項以降を無視します。

式(1)・(2)の線形化：

式(1)と(2)において$f(\bf{y_{t-1}},\bf{u_t})$と$g(\bf{y_{t}})$を$\bf{\hat{y}_{t-1|t-1}}$の周りでTaylor展開し、2次の項移行を無視します。

$$ \begin{align} {\bf y}_t&=f({ \bf y}_{t-1},{\bf u}_t) \\\ &=f({\bf \hat{y}}_{t-1|t-1},{\bf u_t})+{ \bf F}_t({ \bf y}_{t-1} - {\bf \hat{y}}_{t-1|t-1}) \tag{5} \newline \newline {\bf z_t}&=g({\bf y}_t) \\\ &=g({ \bf \hat{y}}_{t|t-1}) + { \bf H}_t({ \bf y}_t-{ \bf \hat{y}}_{t|t-1}) \tag{6} \end{align} $$

ここで${ \bf F_t,H_t }$はJacobianであり、以下で表されます。

$$ \begin{align} { \bf F_t } &= \left.\frac{\partial f}{\partial \bf{y}}\right|_{\bf{y}=\bf{\hat{y}}_{t-1|t-1},\bf{u_t}} \tag{7} \newline \newline { \bf H_t } &= \left.\frac{\partial g}{\partial \bf{y}}\right|_{\bf{y}=\bf{\hat{y}}_{t|t-1}} \tag{8} \end{align} $$

この関係式を用いて以下は予測モデルと更新モデルの期待値と分散の式を導出します。考え方は線形の場合と同様です。時刻:$t$において得られている情報：$I_t$を使って条件付き確率の期待値・分散として計算します。

予測モデル：

$$ \begin{align} {\bf \hat{y}_{t|t-1} } &= E[{ \bf y_t }| I_{t-1},{ \bf u_t }] \\\ &= E[f({ \bf \hat{y}_{t-1|t-1} },{\bf u_t })+{ \bf F}_t({\bf y_{t-1} } - { \bf \hat{y} }_{t-1|t-1}) + { \bf G_t } { \bf w_t }| I_{t-1},{ \bf u_t}]\\\ &= E[f({ \bf \hat{y}_{t-1|t-1} },{ \bf u_t })| I_{t-1},{ \bf u_t }]+E[{ \bf F}_t({ \bf y_{t-1}} - { \bf \hat{y}}_{t-1|t-1}) | I_{t-1},{ \bf u_t}] + E[{ \bf G_t }{ \bf w_t } | I_{t-1},{ \bf u_t }]\\\ &= f({ \bf \hat{y}_{t-1|t-1}},{ \bf u_t })+{ \bf F}_t({ \bf \hat{y}}_{t-1|t-1} - { \bf \hat{y}}_{t-1|t-1}) \\\ &= f({ \bf \hat{y}_{t-1|t-1}},{ \bf u_t }) \tag{9} \newline \newline { \bf \Sigma_{t|t-1}} &= Var[{ \bf y_t }|I_{t-1},{\bf u_t }] \\\ &= Var[f({ \bf \hat{y}_{t-1|t-1}},{ \bf u_t })+{ \bf F}_t({ \bf y_{t-1}} - { \bf \hat{y}}_{t-1|t-1})+ { \bf G_t }{ \bf w_t } | I_{t-1},{ \bf u_t }]\\\ &= Var[f({ \bf \hat{y}_{t-1|t-1} },{\bf u_t })| I_{t-1},{ \bf u_t }]+Var[{ \bf F}_t({ \bf y_{t-1} } - { \bf \hat{y}}_{t-1|t-1})| I_{t-1},{ \bf u_t }]+ Var[{ \bf G_t }{ \bf w_t } | I_{t-1},{ \bf u_t }] \\\ &=Var[{ \bf F}_t{ \bf y_{t-1} }| I_{t-1},{ \bf u_t }]+{\bf{G_tQ_tG^T_t}} \\\ &={\bf F_t \Sigma_{t-1|t-1} F^T_t}+{\bf{G_tQ_tG^T_t}} \tag{10} \end{align} $$

更新モデル：

$$ \begin{align} {\bf \hat{y}}_{t|t}&=E[{ \bf y_t }|I_{t}] \\\ &= E[{ \bf y_t }|I_{t-1},{ \bf z_t}]\\\ &= E[{ \bf y_{t|t-1} }|{ \bf z_t}]\\\ &= {\bf \hat{y}}_{t|t-1} + {\bf CS^{-1}}({\bf z}_t - g({\bf y_t})) \\\ &={\bf \hat{y}}_{t|t-1} + {\bf K }_t({\bf z}_t - g({\bf y_t})) \tag{11} \newline \newline {\bf \Sigma}_{t|t} &= Var[\bf{y}_t|I_t] \\\ &= Var[{ \bf y_t }|I_{t-1},{ \bf z_t}]\\\ &= Var[{ \bf y_{t|t-1} }|{ \bf z_t}]\\\ &= {\bf \Sigma}_{t|t-1} - \bf{\Sigma}_{t|t-1}H_t^TS^{-1}H_t{\bf \Sigma}_{t|t-1} \\\ & ={\bf (I -K_t H_t) \Sigma}_{t|t-1} \tag{12} \\\newline K_t &= {\bf \Sigma}_{t|t-1}{ \bf H}_t^T { \bf S}^{-1} \tag{13} \end{align} $$

ここで${ \bf C,S}$は以下で表される。これも線形の場合と変わりません。

$$ \begin{align} C &=Cov(\bf{y}_{t|t-1},\bf{z}_t) \\\ &=Cov(\bf{y}_{t|t-1},H_t\bf{y}_{t|t-1}+ v_t) \\\ &=E[(\bf{y}_{t|t-1} - \bf{\hat{y}}_{t|t-1})(H_t\bf{y}_{t|t-1} - H_t\bf{\hat{y}}_{t|t-1})^T] \\\ &=E[(\bf{y}_{t|t-1} - \bf{\hat{y}}_{t|t-1})(\bf{y}_{t|t-1} -\bf{\hat{y}}_{t|t-1})^TH_t^T] \\\ &=E[(\bf{y}_{t|t-1} - \bf{\hat{y}}_{t|t-1})(\bf{y}_{t|t-1} -\bf{\hat{y}}_{t|t-1})^T]H_t^T \\\ &={\bf \Sigma}_{t|t-1}{ \bf H}_t^T \tag{14} \\\ \newline S&= Var({\bf z}_t) \\\ &= Var( { \bf H}_t \bf{y}_{t|t-1}+{ \bf v}_t) \\\ &={ \bf H}_t { \bf \Sigma}_{t|t-1} { \bf H}_t ^T + { \bf R}_t \tag{15} \end{align} $$

以上まとめるとEKFの予測・更新の式は以下の様になります。

予測：

$$ \begin{align} {\bf \hat{y}_{t|t-1} }& = f({ \bf \hat{y}_{t-1|t-1}},{ \bf u_t })\\\ { \bf \Sigma_{t|t-1}} &= {\bf F_t \Sigma_{t-1|t-1} F^T_t}+{\bf{G_tQ_tG^T_t}} \end{align} $$

更新：

$$ \begin{align} {\bf C } &= { \bf \Sigma}_{t|t-1}{ \bf H}_t^T \\\ {\bf S } &= { \bf H}_t { \bf \Sigma}_{t|t-1} { \bf H}_t^T + { \bf R}_t \\\ { \bf K}_t &= \bf{\Sigma}_{t|t-1}H_t^T S^{-1} \\\ \newline {\bf \hat{y}}_{t|t}&={\bf \hat{y}}_{t|t-1} + {\bf K }_t({\bf z}_t - g({\bf y_t})) \\\ {\bf \Sigma}_{t|t} &= ({ \bf I} -{ \bf K}_t { \bf H}_t){ \bf\Sigma}_{t|t-1} \end{align} $$

但し、

$$ \begin{align} { \bf F_t } &= \left.\frac{\partial f}{\partial \bf{y}}\right|_{\bf{y}=\bf{\hat{y}}_{t-1|t-1},\bf{u_t}} \newline \newline { \bf H_t } &= \left.\frac{\partial g}{\partial \bf{y}}\right|_{\bf{y}=\bf{\hat{y}}_{t|t-1}} \end{align} $$

UKF

EKFの課題として、線形化する一点のみの局所的な傾きの情報のみで変換後の分布を決めてしまうので、非線形性が強い場合誤差が大きくなってしまうという課題があります。そこで提案されたのがUKFでEKFと異なり一点のみではなくシグマ点という複数の点を抽出し、それらすべてを使って変換後の分布を求めます(図１)。

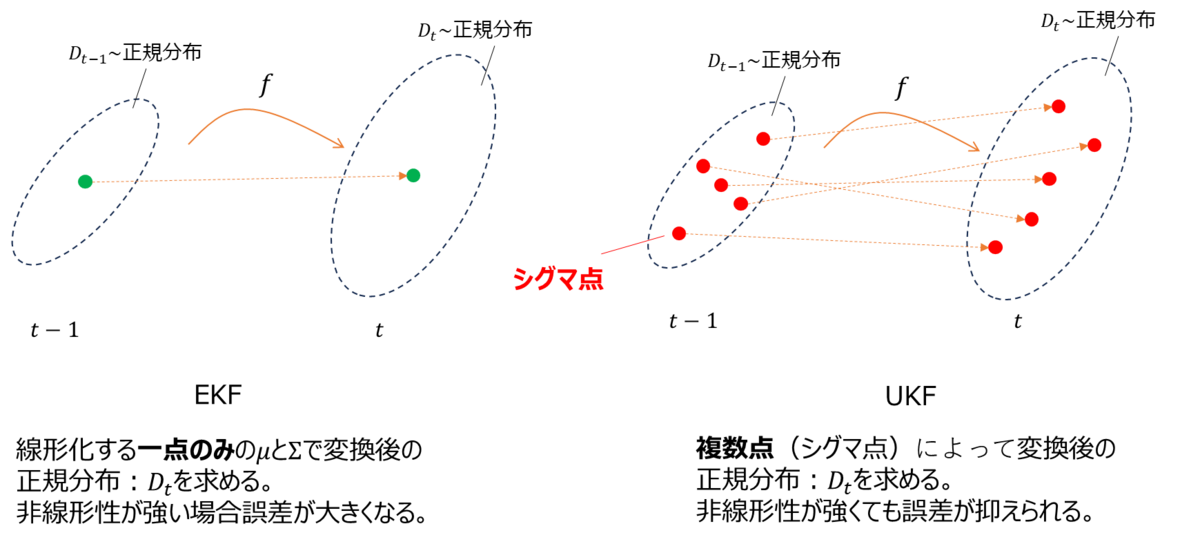
　EKFは非線形変換を式(7),(8)で表したように更新前の状態量の周辺でTyalor展開して近似しました。これは図１の左側のように更新前の状態量一点の傾きのみで決まる変換が分布：$D_{t-1}$全体に適用されると仮定し、変換後の分布：$D_t$を計算します。しかし変換：$f$の非線形性が強い場合は展開した一点に適用される線形変換が分布：$D_{t-1}$のずれた点に対しては適用できず誤差が大きくなってしまうという問題が発生します。

　そこでUKFでは決まったルールに則って抽出したサンプル複数個を$f$によって先に変換し、そのそれぞれの変換後の値を使って変換後の分布:$D_t$を求めます。この決まったルールによって抽出されたサンプル点を”シグマ点”といいます。非線形変換によって変換された点は正規分布には必ずしも従わないのですが、UKFでは変換後のシグマ点がもっとも従う正規分布を求めることで変換後の分布：$D_t$を決定します。

　また、変換後のシグマ点を使って$D_t$を決定する際にすべてを等価に扱うわけではなく一般に中心に近いほど重みを付けて求めます。$D_t$を近似する際に注目する点により重みを付けた近似を行うことは自然な発想かと思います。以下では、このシグマ点の抽出方法と重みについてと分布：$D_t$の導出手順について述べます。

シグマ点の抽出方法：

　シグマ点の設定方法は無数に考えることができますが、その中でもより情報量が高くかつ満遍ない抽出方法を考えます。まずEKFでも代表点としている分布の平均点は含めるべき点であることは直感的にわかります。さらに平均点を中心に標準偏差の定数倍にした点を抽出します。分布を代表する方向を$L$個求めて図2のように各方向の+と-の方向にシグマ点を設定します。図2は$L=2$で合計5つのシグマ点を設定する例です。

一般に$L$個の方向でシグマ点をを取る場合に、$i=1,2,3,...,L$番目の方向のシグマ点：$\chi^{[i]}$は以下で表すことができます。

$$ \begin{align} {\bf \chi}^{[0]}&={\bf \mu} \\\ {\bf \chi}_{+}^{[i]}&={ \bf \mu} +(\sqrt{(L+\lambda){\bf \Sigma }})_i \quad (i=1,2,3,...,L) \\\ {\bf \chi}_{-}^{[i]}&={ \bf \mu} -(\sqrt{(L+\lambda){\bf \Sigma }})_{i-L} \quad (i=L+1,L+2,L+3,...,2L) \end{align} \tag{16} $$

ここで${\bf \mu}$は平均点であり、$(\sqrt{(L+\lambda){\bf \Sigma }})_i$は以前のエントリーでも述べた対角化によって以下のように${ \bf U}$と${ \bf D}$に分解した行列の第$i$列です。

$$ \begin{align} {\bf \Sigma} &={\bf U D U^T} \\\ &={\bf U }\begin{bmatrix} d_{11} & \cdots & 0 \\\ 0 & \ddots & 0 \\\ 0 & \cdots & d_{nn} \end{bmatrix} {\bf U }^T \\\ &={\bf U }\begin{bmatrix} \sqrt{d_{11}} & \cdots & 0 \\\ 0 & \ddots & 0 \\\ 0 & \cdots & \sqrt{d_{nn}} \end{bmatrix} \begin{bmatrix} \sqrt{d_{11}} & \cdots & 0 \\\ 0 & \ddots & 0 \\\ 0 & \cdots & \sqrt{d_{nn}} \end{bmatrix} {\bf U }^T \\\ &={ \bf U \sqrt{D} \sqrt{D}^T U^T } \tag{17} \newline \newline { \bf \sqrt{\Sigma}} &= { \bf U \sqrt{D}} \tag{18} \end{align} $$

なので、$(\sqrt{(L+\lambda){\bf \Sigma }})_i$は上記式(17)・(18)によって導き出される${ \bf \sqrt{\Sigma}}$にスカラー倍の係数：$\sqrt{(L+\lambda)}$をかけたものになります。ここで$\lambda$は調整パラメータになります。

　ところで、シグマ点を抽出するうえでは元の分布：$D_{t-1}$をなるべく代表する点を選びたいという目的がありました。そのために分布の拡がりがある方向に点をとっていくという方法をとります。これは主成分分析(Principle Component Analysis:PCA)において分散共分散行列を対角化することで主成分を求める手順にほかならず、それは式(17)そのものになります。なので、式(17)に登場する$\sqrt{D}$の成分を大きい順に並び変え、第1,2,...,L主成分の固有ベクトルこそが第$i$方向のシグマ点${\bf \chi}_{+}^{[i]},{\bf \chi}_{-}^{[i]}$の方向となる。

この変換された$2L+1$この点：${\bf \chi^{[0]}, \chi}_{+}^{[i]},{\bf \chi}_{-}^{[i]}$に重みを付けて平均と分散は以下のように計算されます。

$$ \begin{align} {\bf \mu'} &= \sum_{n=0}^{2L} w_m^{[i]}g({\bf \chi^{[i]}})\tag{19} \\\ {\bf \Sigma' } &= \sum_{n=1}^{2L} w_c^{[i]}(g({\bf \chi^{[i]}}) - { \bf \mu'})(g({\bf \chi^{[i]}}) - { \bf \mu'})^T \tag{20} \end{align} $$

ここで、$w_m^{[i]}$と$w_c^{[i]}$はそれぞれ平均と分散を求めるための合計が1となるような重み係数で以下のような式で表されます。これらの具体的な式の導出については本稿では割愛させて頂きますが、詳しくは参考文献[2]でも述べられているのでこちらを参照してください。

$$ \begin{align} w_m^{[0]} &= \frac{\lambda}{L + \lambda} \\\ w_c^{[0]} &= w_m^{[0]}-(1-\alpha^2+\beta) \\\ w_m^{[i]} &= w_c^{[i]} = \frac{1}{2(L + \lambda)} (i=1,2,3,...,L) \end{align} \tag{21} $$

式(21)で$\alpha$と$\beta$は調整パラメータです。以下でこれらの関係を用いた予測と更新の手続きでは、(17)と(18)式で抽出方向を求めたうえでシグマ点を決定し、式(21)で決定される重みを用いて式(19)と(20)で平均と分散を求めることを行います。

予測：予測のステップ、つまり${\bf y_{t-1|t-1}}$から${\bf y_{t|t-1}}$を求める手順を整理します。なので、再帰的手続きによって${\bf \hat{y}_{t|t-1} }$と${ \bf \Sigma_{t|t-1}}$は求まっているものとします。この下で式(17)と(18)のPCAの手続きによって抽出されたシグマ点を$s_i(i=1,2,3,...,2L+1)$とします。この時に式(1)の非線形関数$f$によって変換された点を$y_i$とします。

$$ {\bf y}_i = f({\bf s}_i) \quad (i=0,2,3,...,2L) \tag{22} $$

よって式(19)と(20)を用いることにより平均と分散は、

$$ \begin{align} {\bf \hat{y}}_{t|t-1} &= \sum_{i=0}^{2L} w_m^{[i]}{\bf y}_i \tag{23}\\\ {\bf \Sigma}_{t|t-1} &= \sum_{i=0}^{2L} w_c^{[i]}({\bf y}_i-{\bf \hat{y}}_{t|t-1})({\bf y}_i-{\bf \hat{y}}_{t|t-1})^T + {\bf{G_tQ_tG^T_t}}\tag{24} \end{align} $$

で求めることができます。

更新：式(23)と(24)によって予測の${\bf \hat{y}}_{t|t-1}$と${\bf \Sigma}_{t|t-1}$が求まったのでこれからの更新の計算式を導出します。予測と同様に、抽出されたシグマ点を$s_i(i=1,2,3,...,2L+1)$の式(2)の非線形関数$g$によって変換された点を$z_i$とします。

$$ {\bf z}_i = g({\bf s}_i) \quad (i=0,2,3,...,2L) \tag{25} $$

以前のエントリーでも述べたように、多変正規分布の条件付確率$X1|X2$はそれぞれの平均と共分散行列を用いて以下のようになります。

$$ X_1|X_2 \sim N(\mu_1 + \Sigma_{12} \Sigma_{22}^{-1} ({\bf x_2}-{\bf \mu_2}), \Sigma_{11} -\Sigma_{12}\Sigma_{22}^{-1}{\Sigma_{12}}^T) \tag{26} $$

なので今求めたい${\bf y}_{t|t-1}|{\bf z}$はこの関係を使うことにより、式(27)-(32)で求める事が出来ます。

$$ \begin{align} {\bf \hat{z} } &= \sum_{i=0}^{2L} w_m^{[i]}{\bf z}_i \tag{27}\\\ {\bf S } &= \sum_{i=0}^{2L} w_c^{[i]}({\bf z}_i- {\bf \hat{z} })({\bf z}_i -{\bf \hat{z} })^T + {\bf R}_t \tag{28} \\\ {\bf C } &= \sum_{i=0}^{2L} w_c^{[i]}({\bf s}_i- {\bf \hat{y}_{t|t-1} })({\bf z}_i -{\bf \hat{z} })^T \tag{29} \\\ {\bf K}_t &= {\bf C } {\bf S }^{-1} \tag{30} \\\ {\bf \hat{y}}_{t|t} &= {\bf \hat{y}}_{t|t-1} + {\bf K}_t({\bf z} - {\bf \hat{z} } ) \tag{31}\\\ {\bf \Sigma}_{t|t-1} &= {\bf \Sigma}_{t-1|t-1} - {\bf K_tSK_t^T} \tag{32} \end{align} $$

まとめ

　非線形なモデルに対してカルマンフィルターを用いるための方法についてEKFとUKFについて説明しました。一般に非線形性が強い場合にはUKFが性能が良いとされています。理論ばかりつらつらと説明してしまったので、次回のエントリーは今回までに説明したカルマンフィルターについて簡単なサンプルを実装してEKFやUKFの性能差を調べてみたいと思います。