Harris Corner Detectionの解説

内容

　SLAMやsfm等をエッジデバイスで動かす際に、軽量なHarris corner detectionは今なお広く用いられている。なんとなくは理解していたが、コーナー検出のための具体的な発想や式の意味を咀嚼しきれていなかったので記事としてまとめてみた。

　最初にコーナーを検出するためのアイデアを感覚的に捉えて、それを数学的にモデルにするにはどうしたら良いかを後半に記載した。コーナーネスの式の意味がいまいち捉えきれていない初学者等の理解の助けになれば幸いです。

１．コーナ検出とは

　特徴点検出は、画像検索やSLAMなどのコンピュータービジョンのタスクで用いられる基本的な処理の一つである。画像から特徴的な点を抽出し、さらに特徴量を計算して後段処理に繋げることが多い。例えば、連続する画像間の特徴点をトラッキングして姿勢推定をしたり、特徴量の類似度によって似ている画像を検索したりする(図１)。

　特徴点はその名の通り特徴的で何かしら意味がありそうな点で、それらを自動で抽出するアルゴリズムの一つが今回紹介するHarris corner detectionである。画像中での特徴として代表的なのは色と形で、形の特徴としてエッジ、コーナーやブロブなどの幾何的特徴がある（図２）。

　幾何的特徴の中でもコーナー点は扱いやすく、Harris corner detectionはコーナー検出の手法として広く用いられている。

　画像からコーナーとなる点を自動抽出する処理について具体的に考えてみる。大雑把には、画像中の全てのピクセルに対してコーナーっぽさを計算し、コーナーである点とそうでない点の区別を行う。形の特徴は、画像の輝度がどう分布しているか、すなわち輝度の分布パターンとして捉えることができる。そこでコーナー点とそうでない点を区別するために、点周囲の領域内の輝度のパターンの違いを用いる。注目する点を中心とした数ピクセル辺長の正方領域が一般的に用いられ、カーネルと呼ばれる。

　Harris corner detectionでは、画像の局所に登場する形のパターンを図３に示したように平坦、エッジ、コーナーの3つへ分類する。よって、平坦、エッジ、コーナーのそれぞれで正方形の小領域内の輝度のパターンが識別できれば、コーナーを抽出することができる。

　輝度のパターンとして具体的には、輝度が領域内でどう変化するかの変化のパターンを用いる。エッジとコーナーは、どちらも輝度が大きく変化する点だが、変化の仕方に違いがある。一方で平坦な点においては輝度が殆ど変化しない。

　平坦、エッジ、コーナーの輝度変化のパターンを詳細に整理する。輝度の変化は、画像の横と縦方向に輝度のパターンがどう変化するかであり、より具体的には正方形の領域内の輝度の合計の変化量である。図３右に示したように、コーナーとは横方向と縦方向の両方に輝度変化がある点ということが分かる。エッジは横か縦どちらか一方に輝度変化が生じる点である。横方向のエッジは横に動かしても殆ど輝度が変化しないが、縦方向には変化がある。逆に縦方向のエッジは縦方向に動かしても殆ど輝度が変化しないが、横方向には変化がある。平坦方向はどちらに動かしても輝度に変化がない点となる。

　以上で述べたとおり、画像からコーナーを抽出するためには、ある注目する点周辺の正方領域内の輝度変化のパターンを計算し、それらを特定の基準で3つへ分類してコーナーとなる点を選べばよい。図4はHarris corner detectionのフローで、輝度変化のパターンを数学的に記述する“特徴量記述”と、基準に基づいてコーナーを判定する”分類”という２つの処理からなる。Harris corner detectionは頑健で計算効率の高いモデルであり、1988年に発表されてから今なお広く用いられている手法となっている。

２．Harris corner detection

　続いてHarris corner detectionの“特徴量記述”および”分類”方法について詳細に見ていく。

2.1. 局所領域の特徴量記述

　平坦・エッジ・コーナーを特徴付けるのは、輝度の変化の仕方と捉えることができる。平坦な領域では周囲と比較して輝度が殆ど変化しないし、エッジやコーナは周囲と比較して輝度の変化のある領域になっている。この周辺領域との輝度の変化を数学的に表して、分類を行う。

　変化を表すためには、微分という数学の道具が便利で画像の輝度について横と縦方向に微分することで変化の仕方が表せる。

2.1.1. 画像の微分

　画像は2次元なので、横と縦のx,y方向それぞれの輝度の微分： $I_x$ と $I_y$ の値を扱う。注目する画素に対して横幅wと縦幅hのカーネルという矩形領域を定義し、このカーネルの中の輝度の合計値の変化で $I_x$ と $I_y$ を定義する。

　図５はカーネルの横幅wと縦幅hが両方3である場合の例を表しており、x方向とy方向の微分 $I_x$ と $I_y$ はそれぞれの方向に1ピクセル動かしたときのカーネル内の輝度の合計値の差分を計算することで求めることができる。x方向に向けて明るくなるような画像領域であれば $I_x$ は正の値に大きくなるし、段々と暗くなるような画像領域であれば $I_x$ が負の値に大きくなる。

2.1.2. 平坦・エッジ・コーナーのIxとIy

　一旦、境界がx軸とy軸に平行な場合のみを考えて、平坦・エッジ・コーナーそれぞれの場合で輝度の微分： $I_x$ と $I_y$ がどのような値になるかを考えてみる。

平坦領域の場合

　平坦領域の場合、カーネル内の輝度の合計値はx,y方向にカーネルを移動させても変化しない（図６）。よって平坦な領域における点は $I_x I_y= 0$ を満たす点となる。

エッジ領域の場合

　続いてエッジ領域の場合を考える（図７）。エッジに関してはx,y方向のいずれかについては、カーネルを動かすと輝度の合計値が変化するが、一方は変化しない。したがって、 $I_x I_y= 0$ となる領域である。実際はx,y軸方向のいずれかに平行なエッジとは限らないので開店も考慮する必要があるが、それについては後述する。

コーナ領域の場合

　コーナーの場合、x,y方向のどちらに変化させてもカーネル内の輝度の合計値に変化が生じる。したがってコーナのみ $| I_x I_y | \gt 0$ となる領域である（図８）。

2.2. コーナーの判定

2.2.1. 回転の考慮

　ここまででコーナー点とは画像の輝度の変化、すなわち2次元の微分 $I_x$ と $I_y$ を考えたときに $| I_x I_y | \gt 0$ となる点である事が分かった。なので画像中の全てのピクセルに対して $I_x$ と $I_y$ を計算して $| I_x I_y | \gt 0$ で判定すれば良い気がするが話はそう単純ではない。上でも説明したとおりで実際は回転を考慮する必要がある。

　図９は、斜めの場合のエッジで $I_x$ と $I_y$ を計算した場合を表しているが、この場合IxもIyも0ではなく結果 $| I_x I_y | \gt 0$ となってしまっている。

　なのでエッジの方向を考えた上で $I_x$ と $I_y$ を計算してあげる必要があり、図１０はエッジの方向を何らかの方法で見付けた上でエッジ面と平行、垂直な方向にそれぞれx'とy'座標をとり直して $I_x'$ と $I_y'$ を計算した場合を表した図になっている。この場合、 $I_y' \gt 0$ であるが $I_x'=0$ となり、既に述べたxy軸にエッジ面が平行な場合と一致する。

　よって次の興味としては、任意の向きのエッジ面に対してどのようにしてxy座標をx'y'座標に変換する回転を求めるのか、ということとなる。2次元の変換は、一つの2x2行列で表すことができる。2次元の変換は回転と軸方向へのスケール倍の合成なので、任意の変換行列は回転行列とスケール倍の行列へ分解することができる。具体的には後で出てくるのだが、固有値分解によってこの分解を行うことができる。

2.2.2. 対角化による輝度変化方向の同定

　Harris corner detectionの具体的なアルゴリズムに関わる内容について見ていく。Harris corner detectionの大まかな流れは、コーナっぽさの指標となるコーナーネスを数学的に定義し、その大きさによってコーナかコーナでないかの判定を行うという2つのステップからなる。

　これまで見て来たとおり、ある領域に注目してその領域内の輝度の変化量が起こる方向を見る事で平坦領域なのか、エッジなのかコーナなのかが判定できる。しかし、その方向は2.2.1.で見たとおり任意の回転を考慮しなければならない。よって予めその回転方向を知らない状態では、まずはあらゆる方向に手当たり次第動かしたときの輝度の変化量を全て計算して、輝度の変化が大きい方向を後から同定して、回転を求めることが必要になる。

　そこで、harris corner detectionでは注目する点の周辺領域として横幅w、縦幅hのカーネル: $K$ を使い、この $K$ 内のピクセル: $(x, y)$ における輝度: $I(x, y)$ の合計値の変化量を考える。任意の方向 $(u,v)$ に変化させたときの $K$ 内の $I(x, y)$ の変化量 $E(u, v)$ を定義し、これを解析することで回転とコーナーネスを計算する（図１１）。

$E(u, v) = \sum_{(x, y) \in K} { w(x, y) (I(x+u,y+v) - I(x, y))^2}$

ここで、 $w(x, y)$ は輝度の合計値を $K$ 内で計算するときの重み付けの関数である。注目する点に近いほど重み付けを大きくし、遠いほど小さくするのが自然でガウシアン分布が用いられることが多い。 $I(x+u,y+v)$ は2次の項以降を無視したテイラー展開をによる近似を用いると次のようになり、

$I(x+u, y+v) = I(x, y) + I_x u + I_y v$

これを、 $E(u, v)$ の式に代入すると、

$E(u, v)= \sum_{(x, y) \in K} { w(x, y) ( {I_x }^2 u^2 + {I_y}^2 v^2 + 2I_x I_y uv)}$

行列を使って整理すると、

$E(u, v) = \begin{bmatrix} u \; v \end{bmatrix} ( \sum_{(x, y) \in K} { \begin{bmatrix} {I_x}^2 \; I_x I_y \\ I_x I_y \; {I_y}^2 \end{bmatrix}} ) \begin{bmatrix} u \\ v \end{bmatrix}$

ここで、行列 $M$ を定義し、これは方向 $(u, v)$ への変化に対してどれだけ輝度変化が起きるかを表す行列となる。

$M=\sum_{(x, y) \in K} { \begin{bmatrix} {I_x}^2 \; I_x I_y \\ I_x I_y \; {I_y}^2 \end{bmatrix}}$

この $M$ を対角化すると、

$E(u, v)= \begin{bmatrix} u \; v \end{bmatrix} R^T S R \begin{bmatrix} u \\ v \end{bmatrix}$

$E(u, v)= (R \begin{bmatrix} u \\ v \end{bmatrix})^T S ( R \begin{bmatrix} u \\ v \end{bmatrix} )$

ここで $R$ は回転行列で、 $S$ は軸方向へのスケール倍の行列である。

$R$ で回転された新たな座標 $\begin{bmatrix} u' \\ v' \end{bmatrix} = R \begin{bmatrix} u \\ v \end{bmatrix}$ を考えると、

$E(u', v') = \begin{bmatrix} u' \; v' \end{bmatrix} \begin{bmatrix} \lambda_1 \; 0 \\ 0 \; \lambda_2 \end{bmatrix} \begin{bmatrix} u' \\ v' \end{bmatrix}$

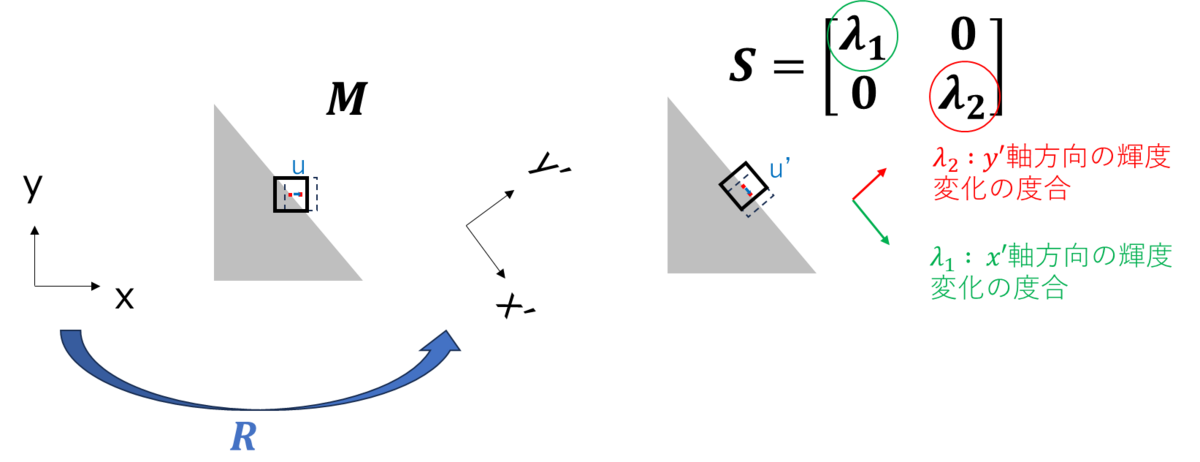
　この $E(u', v')$ は輝度変化が最も起こる方向 $x'$ または $y'$ に対する輝度の変化度合いで、 $\lambda_1$ と $\lambda_2$ はそれぞれの方向に対する輝度の変化度合いということになる（図１２）。したがってここで2.1.2.で述べた平坦・エッジ・コーナーの $x'$ と $y'$ 方向の輝度変化量を考えると、 $\lambda_1$ と $\lambda_2$ が共に大きい場合がコーナーっぽさが強く、どちらか一方のみが大きい場合はエッジっぽさが強いということになる。この $\lambda_1$ と $\lambda_2$ の取る値による平坦・エッジ・コーナーの分布を図示したものが図１３である。

　ここまでの流れを整理すると、画像中の各ピクセルに対して $M$ を計算して対角化を行い、得られた $\lambda_1$ と $\lambda_2$ の値を図１３の境界にあたる閾値によってコーナーか否かを判定するのがコーナー抽出の処理の流れとなる。

2.2.3. コーナーネスの定義

　2.2.2.で述べた方法はピクセル数分の対角化演算が必要で処理が重い。そこでharris corner detectionの大きな貢献として、これまで述べた $\lambda_1$ と $\lambda_2$ の値による判定に相当する判定を、以下の式の値で表されるコーナーネスだけで判定する事ができる点に注目し、処理を大きく軽量化することに成功した。

$C = det(\textbf{M}) - k (tr(\textbf{M}))^2$

ここで、 $det(\textbf{M})$ は行列式、 $tr(\textbf{M})$ はトレースで、kは調整パラメータで経験的に0.04～0.06の値が用いられる。一般に行列式は固有値の積に等しいという性質を用いることで上式は $\lambda_1$ と $\lambda_2$ を用いて下記で表すことができる。

$C = \lambda_1 \lambda_2 - k (\lambda_1 + \lambda_2)^2$

　このコーナネスCを用いることで、 $det(M)$ と $tr(M)$ を計算するだけで、2.2.2.でみたピクセルごとの固有値分解の計算をしなくて済む。図１４に $\lambda_1$ と $\lambda_2$ に対するCの分布を示す。図１３の対応をみるとCが大きければコーナーである事が分かり、Cをコーナネスとして用いることができることが分かる。具体的には、閾値thを設定し、C > thとなるピクセルとコーナーとして抽出する。 $\lambda_1$ と $\lambda_2$ を対角化によって求めずとも、 $C = det(\textbf{M}) - k (tr(\textbf{M}))^2$ によって直接計算した $C$ を用いれば、コーナーの判定を行うことができる。

3. まとめ

　輝度の変化のパターンに注目し、画像中の領域を平坦・エッジ・コーナーの三つに分類してコーナーネスを定義する考え方について述べた。画像の微分 $I_x$ と $I_y$ を用いて2x2の行列の成分を解析することで平坦・エッジ・コーナーが分類できるが回転を考慮するためには固有値解析を行う必要があることを確認した。

　Harris corner detectionはこの考え方に従いつつ、演算量の大きいピクセル毎の固有値解析を避けるためにコーナーネスを定義し、その単純な閾値判定によってコーナー抽出が行える手法を提案した。このコーナーネスの考え方は、SIFTにおける安定したキーポイントの絞り込みにも応用されており、特徴点検出において重要な考え方の一つである。

4. 参考文献

画像認識 (機械学習プロフェッショナルシリーズ), 原田達也著, 2017
OpenCV: Harris corner detector

BIOCV’s blog